Deriving the Catenary Curve Equation
A catenary curve describes the shape the displacement cable takes when subjected to a uniform force such as gravity. This curve is the shape of a perfectly flexible chain suspended by its ends and acted on by gravity. The equation was obtained by Leibniz and Bernoulli in 1691 in response to a challenge by Bernoulli and Jacob.
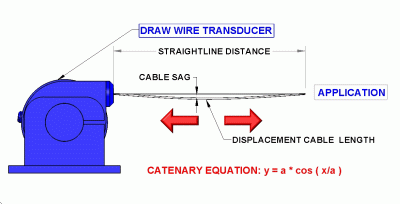
Displacement Cable Idealized As A Catenary Curve
The equation of a catenary curve can be derived by examining a very small part of a cable and all forces acting on it (see Figure 2)

Figure 2 - Forces Acting on a Part of Cable (Section 1-2)
Here h is the sag the cable gets under the action of gravitational force. To simplify, we will examine two points on the cable: points 1 and 2. Let the distance between point 1 and 2 be
so small, that cable segment 1-2 is linear. Let dx and dy be projections of section 1-2
length to X and Y axes respectively.
A tightening force is acting at every point of cable. It is directed at a tangent to cable curve and
depends only on the coordinates of cable point. Let the tightening force at point 1 be N and that at point 2 be N+dN, where dN is a small addition due to difference of coordinates.
Let P be the weight of cable section 1-2. Weight is directed downwards, parallel to Y
axis. Let α be the angle between the X axis and cable section 1-2.
For cable section 1-2 to be at rest and equilibrium with the rest of cable, forces acting on this section need to balance each other. The sum of these forces need to equal to zero.
| Formula |
Explanation |
 |
Projections of sum of all forces acting at section 1-2 to X and Y axes should look like formula 1. Here Nx and Ny are projections of tighting force N to X an Y axes correspondingly. These equations give us the value for cable weight P (formula 2).
|
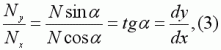 |
We see from Figure 2 that the ratio of tighting force projections (N) is found to be a slope ratio
of the force N (see formula 3).
|
 |
If we differentiate this ratio by x, we get second derivative of ratio (formula 4).
|
 |
At the same time, cable weight P is cable weight per unit length (q) mutliplied by differential of
arc (dS) (formula 5).
|
 |
Using formula 2, we can see that first derivative of projecting of tightening force to Y axis can
be showed by the differential of arc (formula 6).
|
 |
If we state formula 7,
|
 |
we get the final equation for cable form (formula 8).
|
 |
We will solve this
equation using substitution (formula 9).
|
 |
Finally we get (formula 10), where C1 and C2 are coefficients that are defined by point of origin in concerned system. We assume this point to be the lowest point of cable, then C1 = 0 and C2 = 1.
|
 |
Hence the equation of cable form looks like formula 11. This formula is
wide-known as that for the catenary curve.
|
 |
Cable sag (h) is value of cable form equation for point l/2 (formula 12), where l is the straightline distance between the position transducer and the application (Figure 1).
|
 |
For cable length, we will use the formula for the length of the catenary curve (formula 13).
|
 |
The length of the cable is the catenary length from point -l/2 to point l/2 (formula 14).
|
Table 1: Derivation of the Catenary Curve Equation
Proving the Calculator
Now some test to prove our calculator above. The input data we have is:
| Field |
Sybmol |
Units |
Default value |
| Cable tension |
Nx |
N |
3 |
| Straightline distance |
l |
m |
0.5 |
| Cable mass per unit length |
|
kg/m |
0.00065617 |
| Force perpendicular to cable length (acceleration of gravity) |
g |
m/s^2 |
9.81 |
For these default inputs, we can use formulas 7-14 to calculate the cable sag and cable length:
| Variable |
Formula |
Value |
| q |
Cable mass per unit length * Force perpendicular to cable length |
0.0064370277 |
| a |
(7) |
466.053610426439519593 |
| Cable sag h |
(12) |
0.00006705237348283384 |
| Cable length S |
(14) |
0.50000002397877673999 |
Because the mass of the cable per unit length is so small and the cable tension is relatively high, cable sag does not produce any significant error unless the cable length is exceptionally long (over 60 feet (18.28 meters)). The cable sag error is minor compared to other error sources (generally less than ± 0.0025%).
The easy-to-use calculator above shows how displacement cable sag affects the accuracy of our position transducers. The calculator displays the cable sag in absolute units as well as a percentage of total cable length ("measurement error").
There is virtually no cable sag error when the displacement cable has no appreciable "side loads" on it such as what exists in a space environment or when the cable is oriented parallel to the direction of gravity.
Other catenary facts:
- Jungius disproved Galileo's claim that the curve of a chain hanging under gravity would be a parabola in 1669.
- The word catenary is derived from the Latin word for "chain."
- The curve is also called the Alysoid and Chainette.
Additional information on the catenary curve can be found at:
Other calculators:
No Warranties: This calculator and information are provided "as is" without any warranty, condition, or representation of any kind, either express or implied, including but not limited to, any warranty respecting non-infringement, and the implied warranties of conditions of merchantability and fitness for a particular purpose. In no event shall SpaceAge Control, Inc. be liable for any direct, indirect, special, incidental, consequential or other damages howsoever caused whether arising in contract, tort, or otherwise, arising out of or in connection with the use or performance of the information contained on this Web page.